1 Introduction
In my most recent publications, I have dealt extensively with individual topics in the field of cluster analysis. This post should serve as a summary of the topics covered.
2 Roadmap for Cluster Analysis
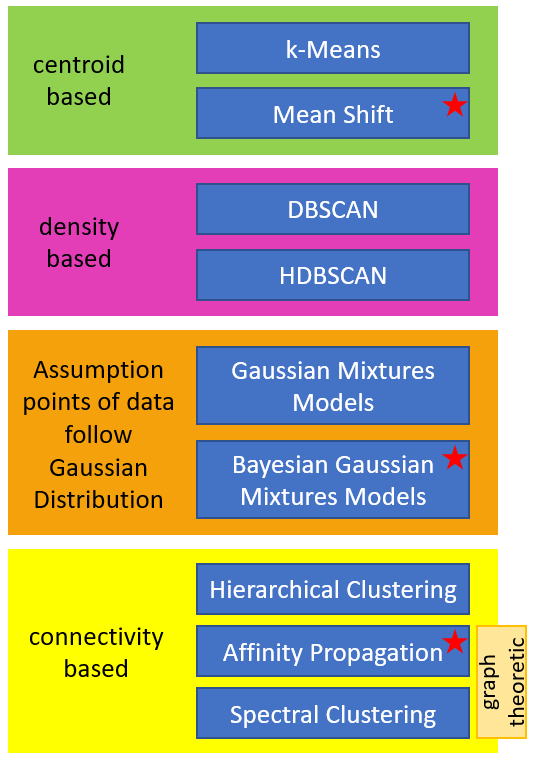
First annotation: The cluster algorithms that are marked with a red star in the graphic do not require an entry of k for the number of clusters
Second annotation: Mean Shift Clustering and Affinity Propagation are not suited for large datasets due to their computational complexity.
Third annotation: Spectral Clustering does not scale well to large numbers of instances and it does not behave well when the clusters have very different size.
Here are the links to the individual topics.
3 Description of the cluster algorithms in a nutshell
k-Means Clustering
The k-Means algorithm starts with a first group of randomly selected centroids, which are used as the beginning points for every cluster, and then performs iterative (repetitive) calculations to optimize the positions of the centroids.
Mean Shift Clustering
The Mean Shift algorithm starts by placing a circle centered on each instance, then for each circle it computes the mean of all the instances located within it and it shifts the circle so that it is centered on the mean. Next, it iterates this mean shifting step until all the circles stop moving. The Means Shift algorithm shifts the circles in the direction of higher density until each of them has found a local density maximum.
DBSCAN
The DBSCAN algorithm defines clustes as continuous regions of high density.
HDBSCAN
The HDBSCAN algorithm can be seen as an extension of the DBSCAN algorithm. The difference is that a hierarchical approach is also pursued here.
Gaussian Mixture Models
A Gaussian Mixture Model (GMM) is a probalistic model that assumes that the instances were generated from a mixture of several Gaussian distributions whose parameters are unknown.
Bayesian Gaussian Mixture Models
A Bayesian Gaussian Mixture Model is quite similar to the GMM model. In the Bayesian GMM the cluster parameters (including the weights, means and covariance metrics) are not treated as fixed model parameters anymore, but as latent random variables, like the cluster assignments.
Hierarchical Clustering
The agglomerative approach of hierarchical clustering builds cluster from the bottom up. At each iteration, agglomerative clustering connects the nearest pair of clusters.
Affinity Propagation
The Affinity Propagation algorithm uses a voting system, where instances vote for similar instances and once the algorithm converges, each representative and its voters form a cluster.
Spectral Clustering
The Spectral Clustering algorithm takes a similarity matrix between the instances and creates a low-dimensional embedding from it. Then it uses another cluster algorithm in this low-dimensional space (i.e. k-Means). The Spectral Clustering algorithm treats the data clustering as a graph partitioning problem without make any assumption on the form of the data clusters.
4 Conclusion
Another large chapter in the field of data science is coming to an end. In this post, I gave a clear overview of which cluster algorithms exists and also gave a brief description of each algorithm.