1 Introduction

In my last post about Deep Learning with the Multi-layer Perceptron, I showed how to make classifications with this type of neural network.

However, an MLP can also be used to solve regression problems. This will be the content of the following post.

For this publication the dataset House Sales in King County, USA from the statistic platform “Kaggle” was used. You can download it from my “GitHub Repository”.

2 Loading the libraries and data

import pandas as pd
import numpy as np

import matplotlib.pyplot as plt

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

from sklearn.neural_network import MLPRegressor

from sklearn import metrics

from sklearn.model_selection import GridSearchCV

df = pd.read_csv('house_prices.csv')
df = df.drop(['id', 'date', 'yr_built', 'yr_renovated', 'zipcode', 'lat', 'long'], axis=1)
df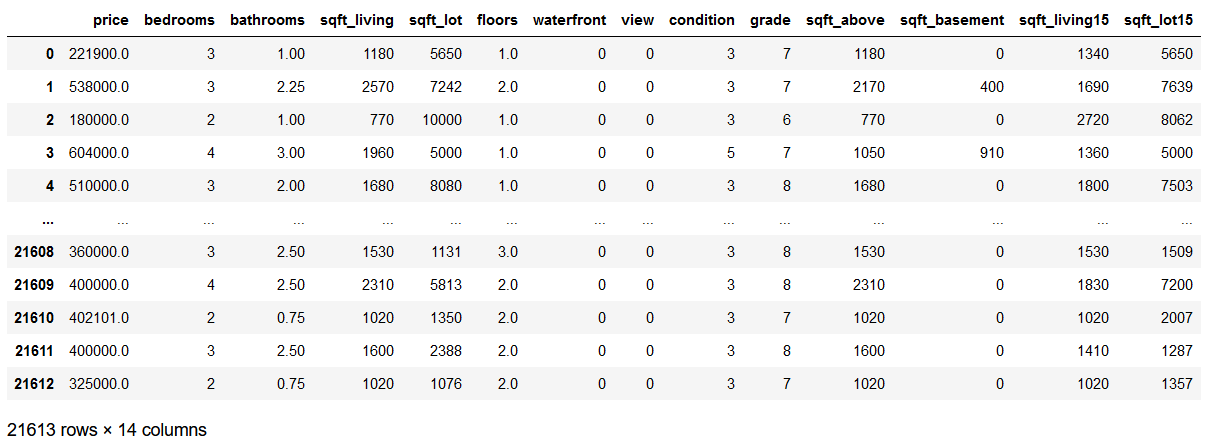

3 Data pre-processing

x = df.drop('price', axis=1)
y = df['price']

trainX, testX, trainY, testY = train_test_split(x, y, test_size = 0.2)

sc=StandardScaler()

scaler = sc.fit(trainX)
trainX_scaled = scaler.transform(trainX)
testX_scaled = scaler.transform(testX)

4 MLPRegressor

mlp_reg = MLPRegressor(hidden_layer_sizes=(150,100,50),
                       max_iter = 300,activation = 'relu',
                       solver = 'adam')

mlp_reg.fit(trainX_scaled, trainY)

5 Model Evaluation

y_pred = mlp_reg.predict(testX_scaled)

df_temp = pd.DataFrame({'Actual': testY, 'Predicted': y_pred})
df_temp.head()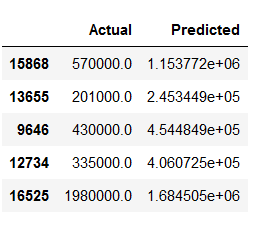

df_temp = df_temp.head(30)
df_temp.plot(kind='bar',figsize=(10,6))
plt.grid(which='major', linestyle='-', linewidth='0.5', color='green')
plt.grid(which='minor', linestyle=':', linewidth='0.5', color='black')
plt.show()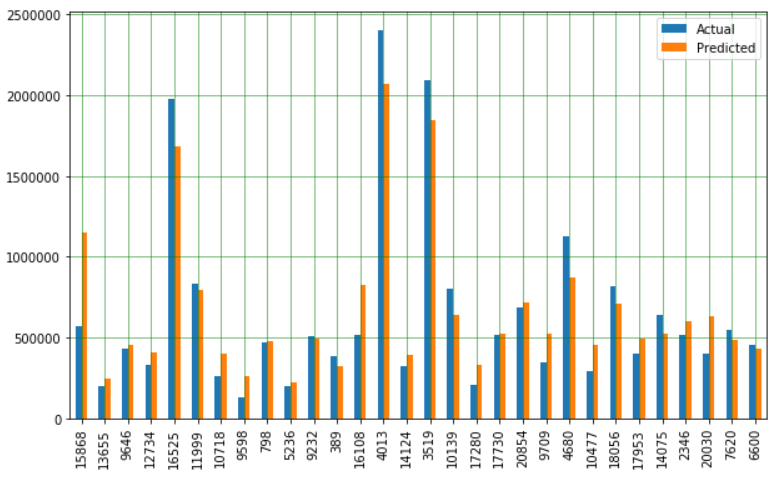

print('Mean Absolute Error:', metrics.mean_absolute_error(testY, y_pred))  
print('Mean Squared Error:', metrics.mean_squared_error(testY, y_pred))  
print('Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(testY, y_pred)))

What these metrics mean and how to interpret them I have described in the following post: Metrics for Regression Analysis

plt.plot(mlp_reg.loss_curve_)
plt.title("Loss Curve", fontsize=14)
plt.xlabel('Iterations')
plt.ylabel('Cost')
plt.show()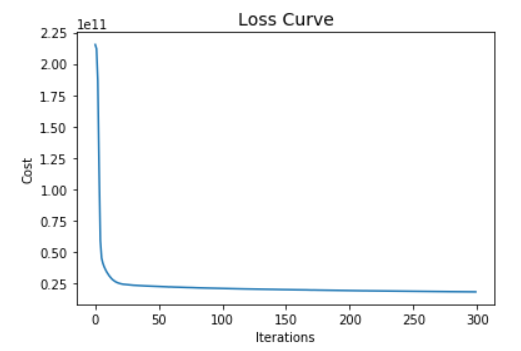

6 Hyper Parameter Tuning

param_grid = {
    'hidden_layer_sizes': [(150,100,50), (120,80,40), (100,50,30)],
    'max_iter': [50, 100],
    'activation': ['tanh', 'relu'],
    'solver': ['sgd', 'adam'],
    'alpha': [0.0001, 0.05],
    'learning_rate': ['constant','adaptive'],
}

grid = GridSearchCV(mlp_reg, param_grid, n_jobs= -1, cv=5)
grid.fit(trainX_scaled, trainY)

print(grid.best_params_)

grid_predictions = grid.predict(testX_scaled)

df_temp2 = pd.DataFrame({'Actual': testY, 'Predicted': grid_predictions})
df_temp2.head()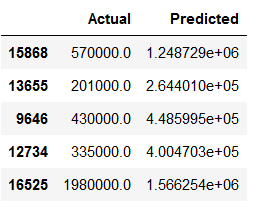

df_temp2 = df_temp2.head(30)
df_temp2.plot(kind='bar',figsize=(10,6))
plt.grid(which='major', linestyle='-', linewidth='0.5', color='green')
plt.grid(which='minor', linestyle=':', linewidth='0.5', color='black')
plt.show()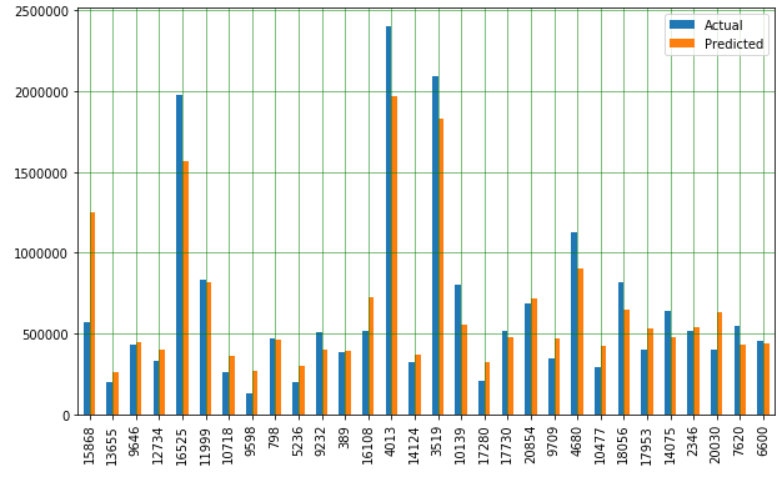

print('Mean Absolute Error:', metrics.mean_absolute_error(testY, grid_predictions))  
print('Mean Squared Error:', metrics.mean_squared_error(testY, grid_predictions))  
print('Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(testY, grid_predictions)))