1 Introduction
Feature selection is pretty important in machine learning primarily because it serves as a fundamental technique to direct the use of variables to what’s most efficient and effective for a given machine learning system.
There are three types of feature selection:
In the following, we will discuss different wrapper methods. Before that, however, there is a short theoretical wrap-up to the filter methods. The embedded methods will be treated in a subsequent publication.
For this post the dataset Santandar Customer Satisfaction (only the train-part) from the statistic platform “Kaggle” was used. You can download it from my GitHub Repository.
2 Loading the libraries and the data
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.feature_selection import VarianceThreshold
from sklearn.ensemble import RandomForestRegressor
#for chapter 4.2.1
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_regression
#for chapter 4.2.2 and 4.2.3
from mlxtend.feature_selection import SequentialFeatureSelector
#for chapter 4.2.4
from sklearn.feature_selection import RFE
from sklearn.linear_model import LinearRegressionsantandar_data = pd.read_csv("path/to/file/santandar.csv")santandar_data.shape
3 Wrap up: Filter methods

Image Source: “Analytics Vidhya”
Filter methods relies on the general uniqueness of the data to be evaluated and pick feature subset, not including any mining algorithm. Filter method uses the exact assessment criterion which includes distance, information, consistency and dependency.
The following filter methods should be considered when creating your regression model:
4 Wrapper methods
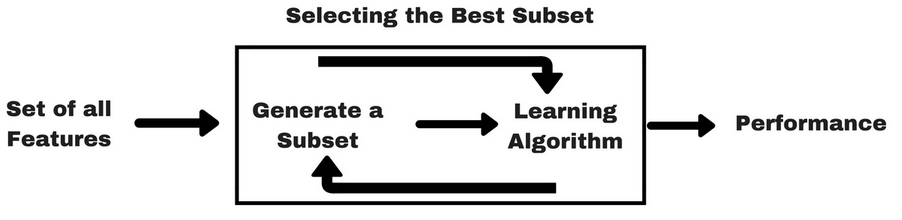
Image Source: “Analytics Vidhya”
For wrapper methods, the feature selection process is based on a specific machine learning algorithm that is to be applied to a particular record. It follows a greedy search approach by evaluating all possible combinations of features based on the evaluation criterion.
Difference between filter and wrapper methods
Well, it might get confusing at times to differentiate between filter and wrapper methods in terms of their functionalities. Let’s take a look at what points they differ from each other:
Filter methods do not incorporate a machine learning model in order to determine if a feature is good or bad whereas wrapper methods use a machine learning model and train it the feature to decide if it is essential for the final model or not.
Filter methods are much faster compared to wrapper methods as they do not involve training the models. On the other hand, wrapper methods are computationally costly, and in the case of massive datasets, wrapper methods are probably not the most effective feature selection method to consider.
Filter methods may fail to find the best subset of features in situations when there is not enough data to model the statistical correlation of the features, but wrapper methods can always provide the best subset of features because of their exhaustive nature.
Using features from wrapper methods in your final machine learning model can lead to overfitting as wrapper methods already train machine learning models with the features and it affects the true power of learning.
Types of wrapper methods
In the following wrapper methods will be presented:
SelectKBest
Select features according to the k highest scores.
Forward Selection
The procedure starts with an empty set of features. The best of the original features is determined and added to the reduced set. At each subsequent iteration, the best of the remaining original attributes is added to the set.
Backward Elimination
The procedure starts with the full set of features. At each step, it removes the worst attribute remaining in the set.
Recursive Feature Elimination
The procedure is almost the same as in the case of backward elimination. Almost … The advantage of RFE is that it works much faster.
4.1 Data Preparation
4.1.1 Check for missing values
def missing_values_table(df):
# Total missing values
mis_val = df.isnull().sum()
# Percentage of missing values
mis_val_percent = 100 * df.isnull().sum() / len(df)
# Make a table with the results
mis_val_table = pd.concat([mis_val, mis_val_percent], axis=1)
# Rename the columns
mis_val_table_ren_columns = mis_val_table.rename(
columns = {0 : 'Missing Values', 1 : '% of Total Values'})
# Sort the table by percentage of missing descending
mis_val_table_ren_columns = mis_val_table_ren_columns[
mis_val_table_ren_columns.iloc[:,1] != 0].sort_values(
'% of Total Values', ascending=False).round(1)
# Print some summary information
print ("Your selected dataframe has " + str(df.shape[1]) + " columns.\n"
"There are " + str(mis_val_table_ren_columns.shape[0]) +
" columns that have missing values.")
# Return the dataframe with missing information
return mis_val_table_ren_columnsmissing_values_table(santandar_data)
As we can see there are no missing values.
4.2 Syntax for wrapper methods
4.2.1 SelectKBest
As already mentioned several times, the most wrapper methods are computationally expensive. Therefore, it is worthwhile to use SelectKBest to select the k best features.
selector = SelectKBest(score_func=f_regression, k=20)
selector.fit(trainX_clean, trainY)
vector_names = list(trainX_clean.columns[selector.get_support(indices=True)])
print(vector_names)
The k determines how many best features should be output. Then the output features are assigned to a new test and train X.
trainX_best = trainX_clean[vector_names]
testX_best = testX_clean[vector_names]
print(trainX_best.shape)
print(testX_best.shape)
To simplify matters, the twenty selected columns are limited to 10.000 lines.
trainX_reduced = trainX_best.iloc[0:10000,]
testX_reduced = testX_best.iloc[0:10000,]
trainY_reduced = trainY.iloc[0:10000,]
testY_reduced = testY.iloc[0:10000,]
print(trainX_reduced.shape)
print(testX_reduced.shape)
print(trainY_reduced.shape)
print(testY_reduced.shape)
4.2.2 Forward Feature Selection
feature_selector = SequentialFeatureSelector(RandomForestRegressor(n_jobs=-1),
k_features=5,
forward=True,
verbose=2,
scoring='r2',
cv=4)With k_features we determine how many features from the remaining twenty should be selected. Here: 5
features = feature_selector.fit(np.array(trainX_reduced), trainY_reduced)The following 5 features were selected by the algorithm:
filtered_features= trainX_reduced.columns[list(features.k_feature_idx_)]
filtered_features
Then these selected features can be assigned to a new X again.
New_train_x = trainX_reduced[filtered_features]
New_test_x = testX_reduced[filtered_features]4.2.3 Backward Elimination
The backward elimination functions almost identically from the syntax. the only difference is that the parameter forward is set to false.
feature_selector = SequentialFeatureSelector(RandomForestRegressor(n_jobs=-1),
k_features=5,
forward=False,
verbose=2,
scoring='r2',
cv=4)features = feature_selector.fit(np.array(trainX_reduced), trainY_reduced)filtered_features= trainX_reduced.columns[list(features.k_feature_idx_)]
filtered_features
New_train_x = trainX_reduced[filtered_features]
New_test_x = testX_reduced[filtered_features]4.2.4 Recursive Feature Elimination (RFE)
The syntax for RFE is now a little different but not particularly complicated. The parameter determining the number of features to extract is here n_features_to_select.
lr = LinearRegression()
rfe = RFE(lr, n_features_to_select=5)
rfe.fit(trainX_reduced,trainY_reduced)With the following two codes we get a statement about which given feature seems to be the best one for the final model:
rfe.support_
rfe.ranking_
For better interpretability, you can simply print the following overview. RFE_support indicates if a feature has been selected (true) or not (false). The ranking is self-explanatory.
If a feature was identified as most suitable, it has an RFE_support ‘true’ and RFE_ranking ‘1’
Columns = trainX_reduced.columns
RFE_support = rfe.support_
RFE_ranking = rfe.ranking_
dataset = pd.DataFrame({'Columns': Columns, 'RFE_support': RFE_support, 'RFE_ranking': RFE_ranking}, columns=['Columns', 'RFE_support', 'RFE_ranking'])
dataset
With the following syntax the final features can be output and assigned to a new x.
df = dataset[(dataset["RFE_support"] == True) & (dataset["RFE_ranking"] == 1)]
filtered_features = df['Columns']
filtered_features
New_train_x = trainX_reduced[filtered_features]
New_test_x = testX_reduced[filtered_features]5 Conclusion
This post discussed the differences between filter methods and wrapper methods. Furthermore, four wrapper methods were shown how they can be used to determine the best features out of a record.
One final note: the wrapper methods shown served as feature selection for regression models. For classification tasks you have to change some parameters. I’ll show in a later post.
